Algoritam trokut-trokut

U prethodnom smo poglavlju vidjeli da nas zanimaju kontakti tipa brid-brid i vrh-lice. Zbog toga ćemo pri detekciji sudara tražiti sudare koji rezultiraju takvim kontaktima. Bez obzira rezultira li sudar kontaktom tipa brid-brid ili vrh-lice, u oba slučaja će se raditi o sudaru dvaju mreža trokuta. To jest, uvijek će se raditi o sudaru dvaju trokuta. Zbog toga ćemo koristiti algoritam koji provjerava sudar između dvaju trokuta.

Definiramo trokut T sa pripadajućim vrhovima V0, V1, i V2. Neka trokut T leži u ravnini π. Jednadžba ravnine π je dana izrazom:

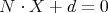
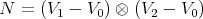
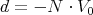
gdje je X bilo koja točka u ravnini π. Udaljenost točke T od ravnine π dobijemo uvrštavanjem točke T u jednadžbu ravnine π.

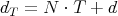
Za dva zadana trokuta T1 i T2, prvi korak ovog algoritma je provjera leže li svi vrhovi jednog trokuta na istoj strani ravnine drugog trokuta. Ukoliko to jest slučaj, algoritam prekida s radom jer ne postoji sudar.

Ako je udaljenost d za sve točke trokuta jednaka nuli, tada se trokuti nalaze u istoj ravnini. Tada trokute projiciramo na ravninu, poravnatu sa osima koordinatnog sustava, za koju su površine dvaju trokuta najveće. Tada za svaki brid trokuta T1provjeravamo intersekciju sa svakim bridom trokuta T2. Ako ni nakon toga sudar nije detektiran, provjeravamo je li jedan od trokuta u potpunosti sadržan unutar drugog. To možemo učiniti tako da za svaki vrh trokuta provjerimo je li unutar drugog trokuta.

Ako su dva trokuta u sudaru, mora postojati linija L smjera N1XN2 koja prolazi kroz oba trokuta. Ako su intervali projekcija dvaju trokuta na ovu liniju u sudaru, tada su i trokuti u sudaru.

Intersekcija dvaju trokuta.

Za zadane trokute T1 i T2: izračunaj jednadžbu ravnine trokuta T2 izađi ako su sve točke trokuta T1 na istoj strani ravnine trokuta T2 izračunaj jednadžbu ravnine trokuta T1 izađi ako su sve točke trokuta T2 na istoj strani ravnine trokuta T1 izračunaj liniju presijecanja L i projiciraj ju na najveću koordinatnu os izračunaj intervale za svaki trokut odredi presjecišta intervala